Olivier Brodier, Toni Neicu, Taimur Ellahi, Kristian Schaadt, and Arshad Kudrolli

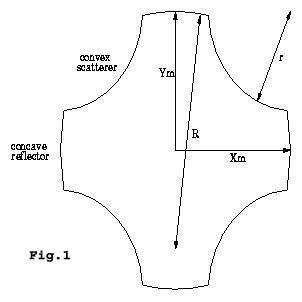
The clover billiard shown in Fig. 1 is an example of a mixed system. The system is called mixed because the corresponding ray dynamics has both chaotic and integrable regions in its phase space. The dimensions that define the clover are the radii of the convex sides r, the radii of the concave sides R, distance between the longitudinal concave sides 2 X_m, and the distance between the vertical concave sides 2 Y_m.

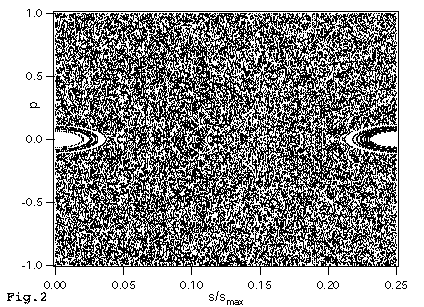
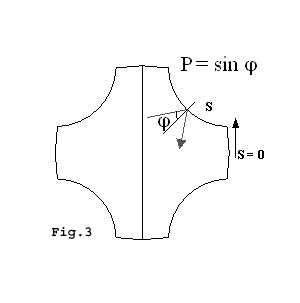
The trajectory of a particle bouncing inside such a clover billiard was numerically simulated. The Poincare surface of section is used to show the phase space explored by the particle. The axis of the plot corresponds to the position and the momentum of the a particle when it hits the Clover boundary. The choice for the selection of phase space coordinates is shown inFig. 3.

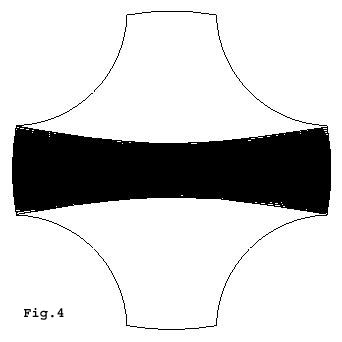
Because the clover has the same symmetry as a square, it is sufficient to plot just one quarter of entire the phase space. In the Poincare surface of section plotted in Fig.2, two main islands are observed that correspond to trajectories which are confined to the vertical and longitudinal focusing areas (see Fig .4). These are the integrable regions. An example of a longitudinal stable trajectory is shown in Fig. 4 .

Beside the integrable regions, large regions covered with random speckles are present in the Fig. 2. These points are generated by trajectories that hit the convex sides and correspond to the chaotic regions. An example of a chaotic trajectory is shown in Fig. 5.

The trajectories that hit only the concave sides are stable and belong to the integrable regions, and trajectories that hit the convex sides are generally chaotic. Another observation which can be made is that the regular regions occupy less area than the chaotic sea and therefore the clover billiard is mainly chaotic. The phase space of the c lover billiard contains both integrable and chaotic regions and therefore such a system is called "mixed".

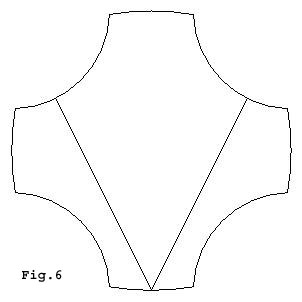
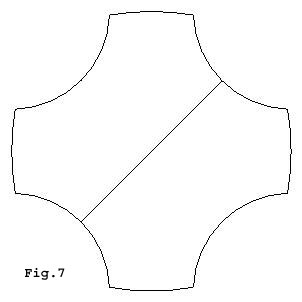
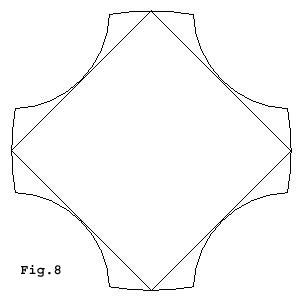
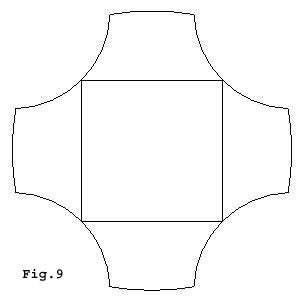
Beside the trajectories that generates the two main regular islands and the chaotic sea there are an infinite number of other stable and unstable trajectories present and some examples are shown in Figs. 6-9.

The nature of the phase space (regular, chaotic, or mixed) is shown to influence the statistics of the spectra of the wave systems. Spectra of completely regular systems ( square or circle billiard) obey the "Poisson" statistics, while spectra of completely chaotic ones (stadium billiard) obey a different statistics the "GOE" (Gaussian Orthogonal Ensemble) statistics. There are very few completely regular or chaotic systems in nature and most systems are the mixed systems. Mixed systems are also more rich compared to the integrable and chaotic limits. In our case we are studying the wave properties of systems with mixed classical phase space by measuring the acoustical eigenvalue spectrum of a clover shaped quartz plate.

Arshad Kudrollii

Last modified: January 19, 2001

Please inform Arshad Kudrolli before using results from these pages.